It is desired to find a three-tap casual filter which gives zero signal as an output to an input of the form
$$x[n]= c_{1}exp\left(-\dfrac{j\pi n}{2}\right)+c_{2}\left(\dfrac{j\pi n}{2}\right),$$
where $c_{1}$ and $c_{2}$ are arbitrary real numbers. The desired three-tap filter is given by
$$h[0]=1,\quad h[1]=a,\quad h[2]=b$$
and
$$h[n]=0\:\: \text{for}\: n<0\: \text{or} \: n>2.$$
What are the values of the filter taps $a$ and $b$ if the output is $y[n]=0$ for all $n$, when $x[n]$ is as given above ?
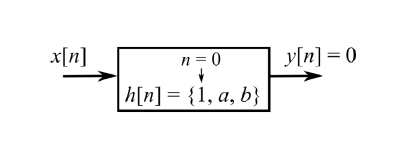
- $a=1,b=1$
- $a=0,b=-1$
- $a=-1,b=1$
- $a=0,b=1$