Consider the line integral
$$\int_{c} (xdy-ydx)$$
the integral being taken in a counterclockwise direction over the closed curve $C$ that forms the boundary of the region $R$ shown in the figure below. The region $R$ is the area enclosed by the union of a $2 \times 3$ rectangle and a semi-circle of radius $1$. The line integral evaluates to
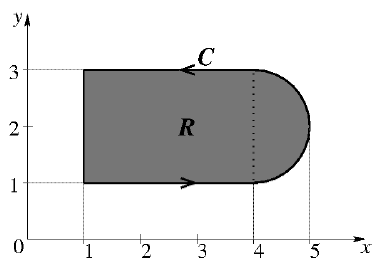
- $6+ \dfrac{\pi}{2}$
- $8+\pi$
- $12+\pi$
- $16+2\pi$