Given that:
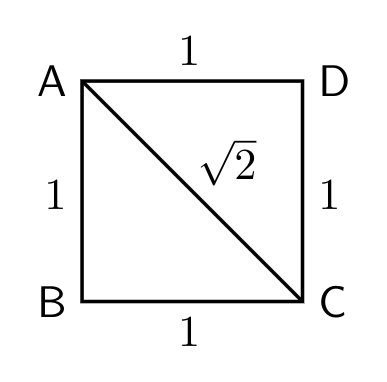
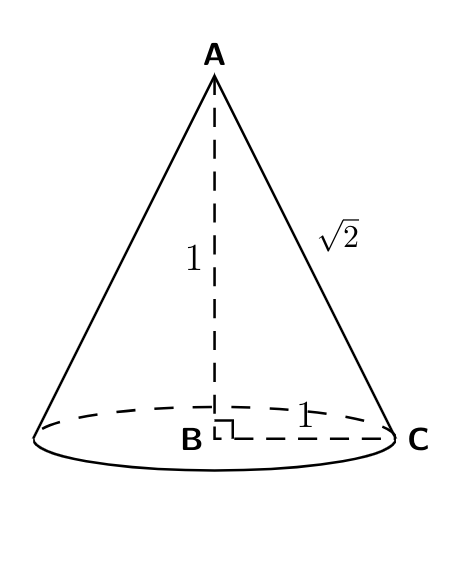
The volume of a cone is $ \dfrac {1} {3} \pi r ^{ 2 } h,$ where $r$ denotes the radius of the base of the cone, and $h$ denotes the height of the cone.
Here, $h = r = 1.$
$\therefore$ The volume of cone $ = \dfrac {1} {3} \pi r ^{ 2 } h = \dfrac{1}{3} \pi (1)^{2} (1) = \dfrac{\pi}{3}$ cubic units.
So, the correct answer is $(A).$