Given that,
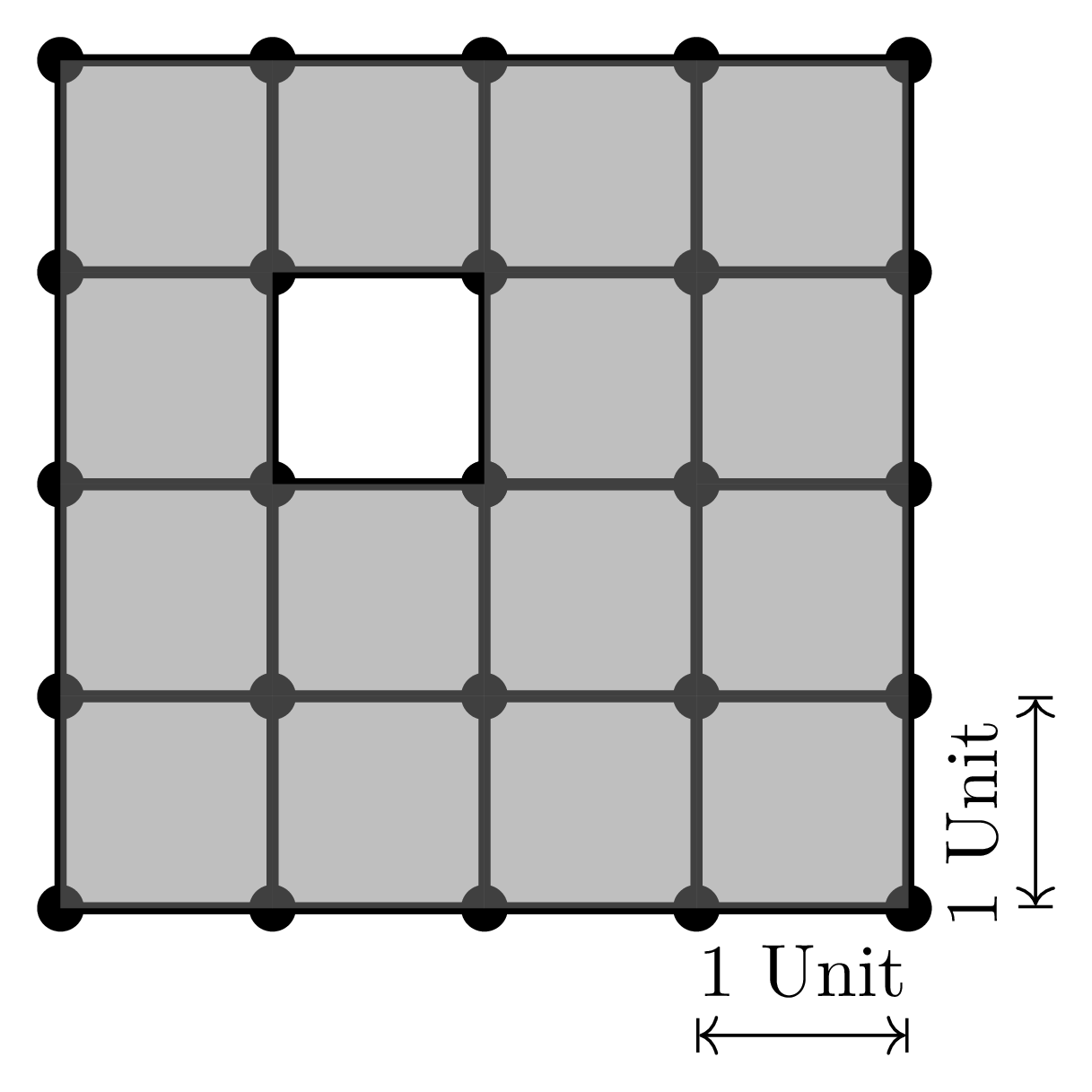
If there is no hole in the $4 \times 4$ grid, then the number of square $ = 1^{2} + 2^{2} + 3^{2} + 4^{2} = 1+4+9+16 = 30$
Now, we can calculate, because of the hole, how many squares are not formed.
- $1 \times 1 = 1$ square
- $2 \times 2 = 4$ squares
- $3 \times 3 = 4$ squares
- $4 \times 4 = 1$ square
$\therefore$ The maximum number of squares without a “hole in the interior” that can be formed within the $4 \times 4$ grid using the unit squares as building blocks $ = 30 – 10 = 20$ squares.
Correct Answer $:\text{B}$
$\textbf{PS:}$ The total number of squares in a $ { n\times n \;\text{grid} = 1^{2} + 2^{2} + 3^{2} + \dots + n^{2} =\frac{n(n+1)(2n+1)}{6}}.$