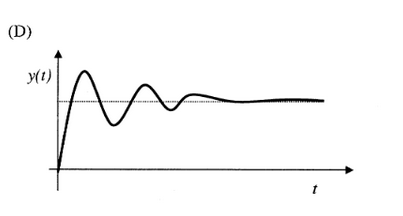
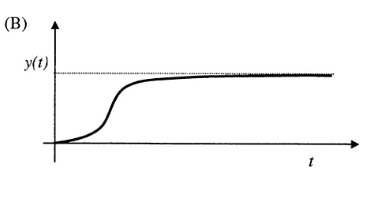
The differential equation $100 \dfrac{d^2 y}{d t^2}-20 \dfrac{d y}{d t}+y=x(t)$ describes a system with an input $x(t)$ and an output $y(t)$. The system, which is initially relaxed, is excited by a unit step input. The output $y(t)$ can be represented by the waveform
-

-
-

-