Statement for Linked Answer Questions 54 and 55:
Consider a baseband binary PAM receiver shown below. The additive channel noise $n(t)$ is white with power spectral density $S_{N}(f)=N_{0} / 2=10^{-20}$ W/Hz. The low-pass filter is ideal with unity gain and cutoff frequency $1 \; \mathrm{MHz}$. Let $Y_{t}$ represent the random variable $y\left(f_{t}\right)$.
\[ \begin{array}{ll}
Y_{t}=N_{k} & \text { if transmitted bit } b_{k}=0 \\
Y_{t}=a+N_{k} & \text { if transmitted bit } b_{k}=1
\end{array}\]
where $N_{k}$ represents the noise sample value. The noise sample has a probability density function. $P_{N_{1}}(n)=0.5 \alpha c^{\cdot \epsilon \text { d.d }}$ (This has mean zero and variance $2 / \alpha^{2}$ ). Assume transmitted bits to be equiprobable and threshold $z$ is set lo a/2 $=10^{-6} \mathrm{~V}$.
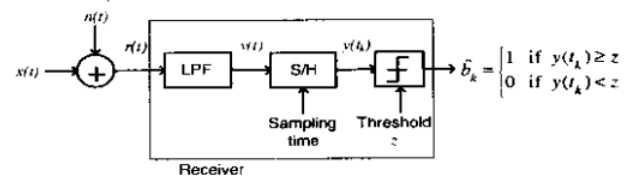
The probability of bit error is
- $0.5 \times e^{-35}$
- $0.5 \times e^{-5}$
- $0.5 \times e^{}$
- $0.5 \times e^{}$