A monochromatic plane wave of wavelength $\lambda = 600 \mu m$ is propagating in the direction as shown in the figure below. $\vec{E_{i}},\vec{E_{r}},$ and $\vec{E_{t}}$ denote incident, reflected, and transmitted electric field vectors associated with the wave.
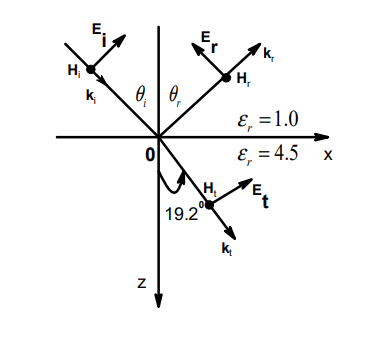
The angle of incidence $\theta_{i}$ and the expression for $\vec{E_{i}}$ are
- $60^{\circ}$ and $\frac{E_{0}}{\sqrt{2}}(\hat{a_{x}} - \hat{a_{z}})e^{-j \frac{\pi\times 10^{4}(x+z)}{3\sqrt{2}}} \:V / m$
- $45^{\circ}$ and $\frac{E_{0}}{\sqrt{2}}(\hat{a_{x}} + \hat{a_{z}})e^{-j \frac{\pi\times 10^{4}z}{3}} \:V / m$
- $45^{\circ}$ and $\frac{E_{0}}{\sqrt{2}}(\hat{a_{x}} - \hat{a_{z}})e^{-j \frac{\pi\times 10^{4}(x+z)}{3\sqrt{2}}} \:V / m$
- $60^{\circ}$ and $\frac{E_{0}}{\sqrt{2}}(\hat{a_{x}} - \hat{a_{z}})e^{-j \frac{\pi\times 10^{4}z}{3}} \:V / m$