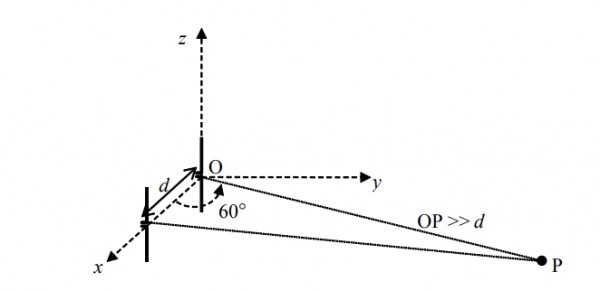
Two half-wave dipole antennas placed as shown in the figure are excited with sinusoidally varying currents of frequency $3\: MHz$ and phase shift of $\frac{\pi}{2}$ between them (the element at the origin leads in phase). If the maximum radiated $E$-field at the point $P$ in the $x-y$ plane occurs at an azimuthal angle of $60^{\circ},$ the distance $d$ (in meters) between the antennas is _________.