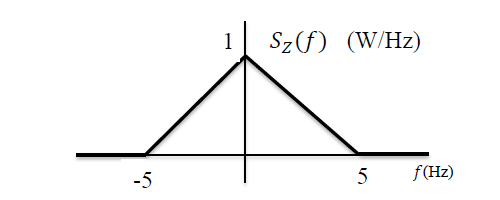Let a random process $Y(t)$ be described as $Y(t)=h(t) \ast X(t)+Z(t),$ where $X(t)$ is a white noise process with power spectral density $S_{x}(f)=5$W/Hz. The filter $h(t)$ has a magnitude response given by $ \mid H(f) \mid =0.5$ for $-5\leq f\leq5,$ and zero elsewhere. $Z(t)$ is a stationary random process, uncorrelated with $X(t)$, with power spectral density as shown in the figure. The power in $Y(t),$ in watts, is equal to _________ $W$ (rounded off to two decimal places).