GATE ECE 2021 | GA Question: 8

Question

Consider a square sheet of side $1$ unit. In the first step, it is cut along the main diagonal to get two triangles. In the next step. one of the cut triangles is revolved about its short edge to form a solid cone. The volume of the resulting cone, in cubic units, is ____________

• A. $\frac{\pi }{3}$
• B. $\frac{2\pi }{3}$
• C. $\frac{3\pi }{2}$
• D. $3\pi$

Answer 1

Given that: 

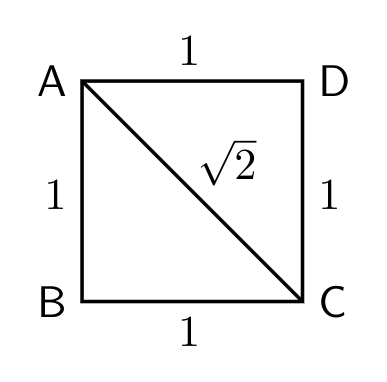
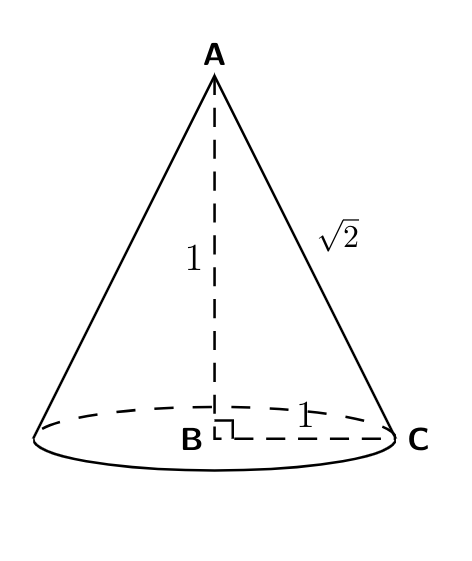
The volume of a cone is $ \dfrac {1} {3} \pi r ^{ 2 } h,$ where $r$ denotes the radius of the base of the cone, and $h$ denotes the height of the cone.

Here, $h = r = 1.$

$\therefore$ The volume of cone $ =  \dfrac {1} {3} \pi r ^{ 2 } h = \dfrac{1}{3} \pi (1)^{2} (1) = \dfrac{\pi}{3}$ cubic units.

So, the correct answer is $(A).$