Given statements are:
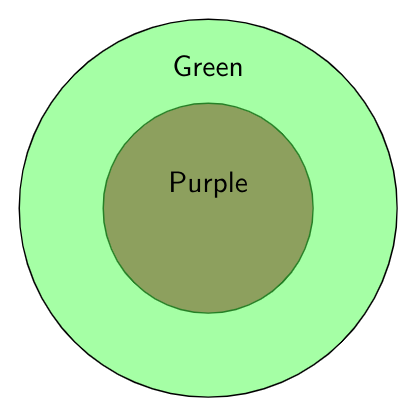
- $\text{Statement 1}$: All purple are green.
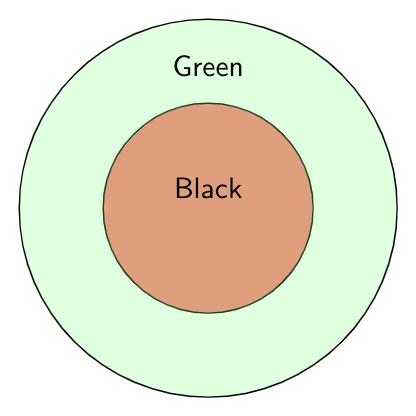
- $\text{Statement 2}$: All black are green.
A conclusion “should always be true”. We can try to make the complement of the conclusion satisfiable (by drawing a Venn diagram) and if we can’t then the conclusion is VALID or else NOT Valid.
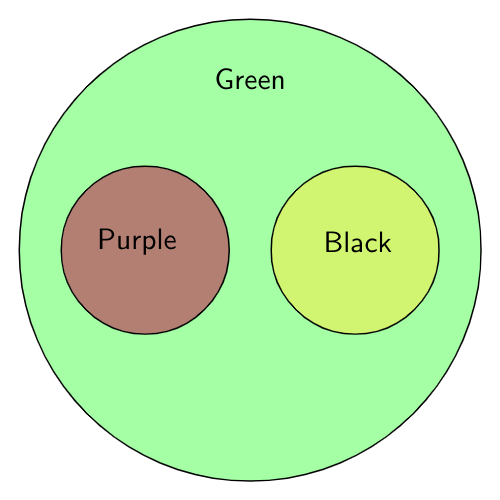
For the first conclusion “Some black are purple” – the complement is “No black is purple”. It is possible as shown below. So the given conclusion is NOT valid.
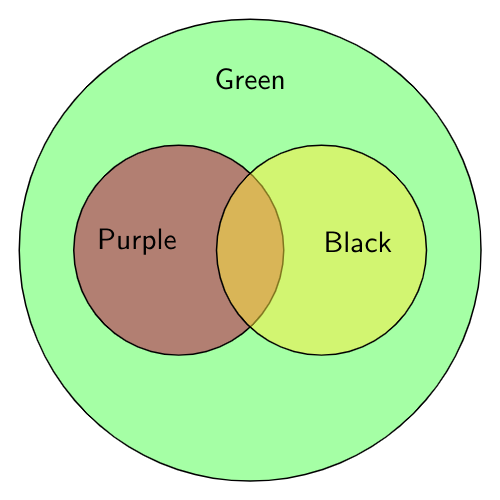
For the second conclusion “No black is purple” – the complement is “Some black is purple”. It is possible as shown below. So the given conclusion is NOT valid.
So, options A, B, and D are false. Option C is correct because we cannot make a Venn diagram making both the conclusions false. If we make conclusion $1$ false, the Venn diagram will satisfy conclusion $2$ and vice versa.
So, the correct answer is $(C).$