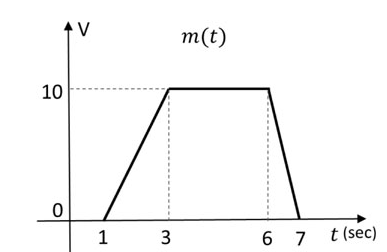
$S_{PM}(t)$ and $S_{FM}(t)$ as defined below, are the phase modulated and the frequency modlated waveforms, respectively, corresponding to the message signal $m(t)$ shown in the figure. $$S_{PM}\left ( t \right )=\cos\left ( 1000\pi t+K_{p}m\left ( t \right )\right ) \\ \text{and } S_{FM}\left ( t \right )=\cos\left ( 1000\pi t+K_{f}\int_{-\infty }^{t}m\left ( \tau \right )d\tau \right )$$ where $K_{p}$ is the phase deviation constant in radians/volt and $K_{f}$ is the frequency deviation constant in radians/second/volt. If the highest instantaneous frequencies of $S_{PM}(t)$ and $S_{FM}(t)$ are same, then the value of the ratio $\dfrac{K_{p}}{K_{f}}$ is ________ seconds.