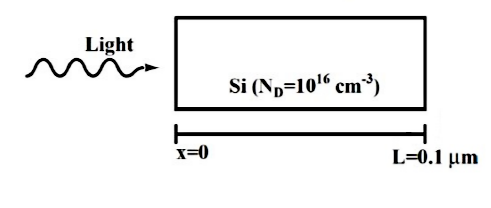
As shown , a uniformly doped Silicon bar of length $L=0.1\mu m$ with a donor concentration $N_{D}=10^{16}cm^{-3}$ is illuminated at $x=0$ such that electron and hole pairs are generated at the rate of $G_{L}=G_{L0}(1-\frac{x}{L}), 0\leq x\leq L$, where $G_{L0}=10^{17}cm^{-3}s^{-1}$ . Hole life time is $10^{-4} s $, electronic charge $q=1.6 \times 10{-19}\, C$,hole diffusion coefficient $D_{p}=100 cm^2/s$ and low level injection condition prevails. Assuming a linearly decaying steady state excess hole concentration that goes to $0$ at $x=L$, the magnitude of the diffusion current density at $x=L/2$, in $A/cm^{2}$, is ___________.