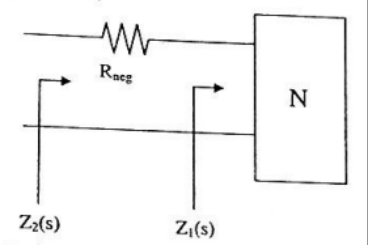
A negative resistance $R_{\text {neg }}$ is connected to a passive network $N$ having driving point impedance $Z_{1}$ (s) as shown below. For $Z_{2}(s)$ to be positive real,
- $\left|\text{R}_{\text {neg }}\right| \leq \operatorname{Re}_{1}(j \omega), \forall \omega$
- $\left|\text{R}_{\text {neg }}\right| \leq\left|Z_{1}(j \omega)\right|, \forall \omega$
- $\left|\text{R}_{\text {neg }}\right| \leq \operatorname{Im} Z_{1}(j \omega), \forall \omega$
- $\left|\text{R}_{\text {neg }}\right| \leq \angle Z_{1}(j \omega), \forall \omega$